|
سرعتِ گروه و محیط
پاشنده در حالت کلی یک بستهی موج را میتوان
بر حسبِ مُدهای فوریه بسط داد:
که در آن Re
قسمت حقیقی را نگه میدارد. چنانچه داشته باشیم
که در آن
عدد
ثابت است تمامی مدهای فوریه با سرعتِ مساوی که همان سرعتِ فاز است منتشر میشوند.
در اینصورت شکل اولیهی موج در طولِ انتشار عوض نمیشود و اصطلاحاً محیط را
غیرپاشنده میگویند. اما اگر بستهگیِ غیر از بالا باشد سرعتِ مُدهای متفاوت یکسان
نیست و هر مُد با سرعتِ فازِ خودش
حرکت میکند. در اینصورت شکلِ
اولیهی موج در محیط عوض میشود و به محیط پاشنده میگویند. در محیطِ پاشنده نمیتوان
به یک بستهی موج یک سرعتِ فازِ یکتا نسبت داد و در عوض یک سرعتِ گروه نسبت میدهند.
فرض کنیم که عمدهی مدهایِ فوریه حولوحوشِ یک عددموجِ
باشند. برایِ راحتی از تابعِ
گاوسی برایِ نمایش این بسته استفاده میکنیم:
فرض میکنیم
به قدری بزرگ باشد تا فقط عددموجهایِ
نزدیکِ
مهم باشند. در اینصورت در
انتگرالِ بالا میتوان بسامد را بسط داد
یا به شکل زیر نوشت:
با این شکل انتگرال با تغییرِ
متغیرِ
به صورتِ زیر در میآید:
که میشود
عبارتِ بالا در واقع یک موجِ تخت
را نشان میدهد که با یک تابعِ گاوسی پوش داده شده است. پوش با سرعتِ
حرکت میکند و البته در طولِ
زمان، به خاطر مخرج کسر در زیرِ رادیکال و در نمائی، پهنشدهگی دارد. به این
سرعت میگویند سرعتِ گروه و در واقع به سرعتِ جابهجائیِ بستهی موج (پوش) است. برای آشنائی هرچه بهتر سه مثال
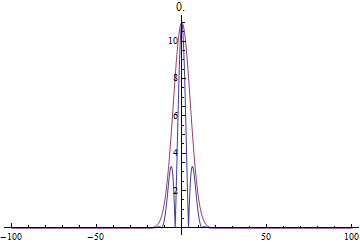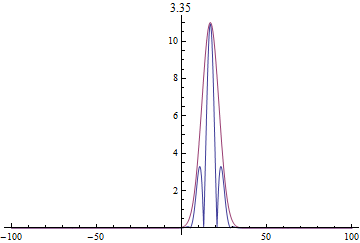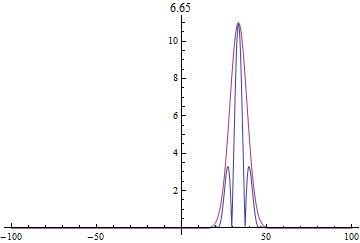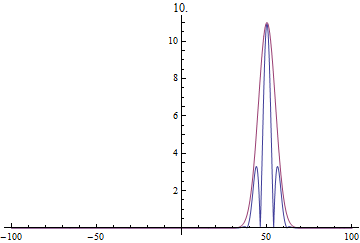
برای انتشار موج در پائین آورده میشود. در تمامیِ شکلها برای نمایش بهتر
قدرمطلق تابعموج رسم شده است. به همین خاطر تمامِ رسمها در بالایِ محور افتادهاند.
در مثالِ اول محیط غیرپاشنده است
و سرعتِ فاز و سرعتِ گروه یکی است. همانطور که در زیر میبینیم شکلِ موج در
طولِ زمان عوض نمیشود.
در مثالِ بعدی فرض شده است که
در شکل علاوه بر قدرمطلقِ تابعموج،
پوش اولیه (رنگ قرمز) با سرعتِ فاز و پوشِ به دست آمده در بالا (رنگ سبز) با
سرعتِ گروه هر دو رسم شدهاند. این سرعتها از عبارتهای زیراند:
همانطور که از روابطِ بالا
انتظار میرود و در شکل دیده میشود پوشِ اولیه با سرعتِ فاز از بستهی موج جلو
میافتد اما پوشِ با سرعتِ گروه همراهِ بسته است. همچنین پهنشدهگیِ تابعموج
مشهود است:
در مثالِ بعدی فرض شده است که
سرعتهای فاز و گروه از عبارتهای
زیراند:
این بار دیده میشود پوشِ اولیه
با سرعتِ فاز از بستهی موج عقب میافتد. مجدداً پهنشدهگیِ تابعموج مشهود
است:
این مثال آخر اتفاقا از نظر
مکانیککوانتومی مهم است. با توجه به روابط
در این صورت سرعت گروه همان سرعت ذره میشود:
مرجع: فیزیک کوانتومی، گاسیوروویچ
|